| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 |
- 프로그래머스
- 한빛미디어
- 3줄 논문
- 입문
- DilatedNet
- TEAM-EDA
- 알고리즘
- eda
- Segmentation
- DFS
- hackerrank
- 엘리스
- 추천시스템
- TEAM EDA
- Image Segmentation
- Python
- 코딩테스트
- 협업필터링
- Object Detection
- Recsys-KR
- 스택
- Machine Learning Advanced
- Semantic Segmentation
- MySQL
- 나는리뷰어다
- 파이썬
- pytorch
- 튜토리얼
- 큐
- 나는 리뷰어다
- Today
- Total
TEAM EDA
교호작용 본문
본 글은 피처 엔지니어링 및 선택 : 예측 모델에 대한 실용적인 접근 방식
(https://bookdown.org/max/FES/detecting-interaction-effects.html)
에서 있는 교호작용 효과 감지라는 내용을 기반으로 다른 자료들을 추가해 정리한 자료입니다.
1. 상호 작용 파생시 고려 사항
교호작용이란 A의 효과가 B의 서로 다른 수준 B1과 B2에서 일관성 있게 나타난다면 두 인자 A, B 간에는 교호작용이 없다고 하고, 만일 B가 ‘B1수준에 있을 때 A의 효과’와 ‘B2수준에 있을 때 A의 효과’간에 차이가 있을 때, A, B 간에 교호작용이 존재한다고 입니다.

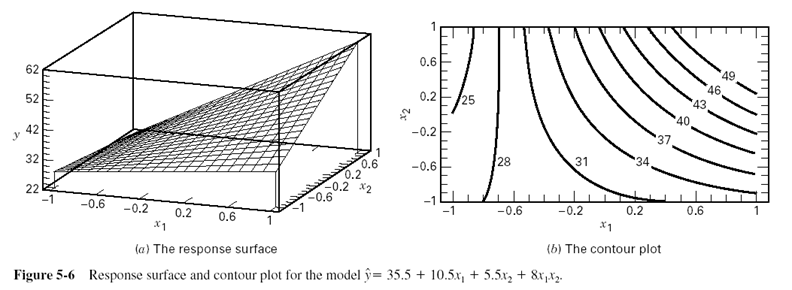
Neter et al.(1996)은 "가능할 때마다 반응 변수에 중요한 방식으로 영향을 줄 수 있는 상호 작용을 미리 식별하는 것이 바람직합니다." 라고 권장합니다. 따라서 전문가가 선택한 상호 작용이 먼저 탐색되어야 합니다. 하지만 많은 상황에서 전문가가 없거나 연구 분야가 새로워서 사전 지식이 없습니다. 이 문제를 해결 한 분야는 통계적 가설 실험입니다.

교화 작용에는 두가지 특징이 있습니다.
첫째, 교호 작용의 수준이 높을수록 교호 작용의 중요성이 낮습니다. 즉, Second Order가 Third Order보다 중요합니다. 이를 계층 구조의 원칙이라고 합니다.
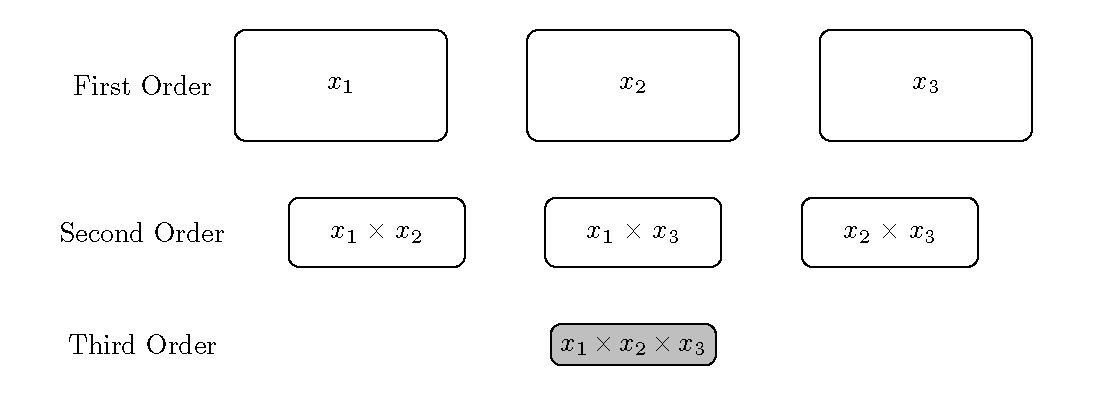
둘째, 교호작용의 중요도는 주효과에 따릅니다. 즉, x1이 중요하면 x1이 들어간 Second Order가 그렇지 않은 Second Order보다 즁요도가 높습니다. 이를 희소성의 원칙이라고 합니다.

상호 작용을 찾는 과정에서, 특히 어떤 용어를 먼저 선별해야하는지 제안 할 전문가 지식이 거의 없거나 전혀 없는 경우 몇가지 실질적인 고려 사항을 해결해야합니다.
- 사용 가능한 데이터를 사용하여 가능한 모든 상호 작용을 열거하고 평가할 수 있습니까?
- 모든 상호작용을 평가해야합니까?
- 예측 변수를 사전 처리하기 전이나 후에 상호 작용 항을 만들어야합니까?
모든 교호 작용을 완전히 열거해야하는지에 대한 질문부터 시작하겠습니다. 희소성의 원칙에 따르면 고차 상호작용보다는 저차의 상호작용이 더 영향을 끼친다고 했습니다. 하지만, 예측 변수의 수가 증가함에 따라 교호 작용 항의 수가 기하 급수적으로 증가합니다. 100개의 예측 변수를 사용하면 4950(100C2)를 평가해야 합니다.
그림 7.6전처리 단계 (a) 이전과 전처리 단계 (b) 이후에 상호 작용 항이 생성 될 때 Stroke Outcome 그룹의 분포를 비교합니다. 전처리 이전의 단계에서는 Outcome의 결과에 따라 분포가 어느 정도 차이를 보이지만 이후에는 그렇지 않는 것을 볼 수 있습니다. 이 사례는 어떤 단계 상호 작용 항을 작성해야하는지 매우 신중해야 함을 보여줍니다. 일반적으로, 상호 작용은 원래 측정 척도에서 가장 타당하고 실질적으로 해석 가능합니다. 따라서 상호 작용 항은 전처리 단계 전에 생성 될 수 있습니다. 이 단계의 순서가 미치는 영향을 확인하는 것이 좋습니다.
2. 예측 상호 작용을 식별하기 위한 무차별 대입 접근법
예측 변수가 적은 경우에는 데이터 세트의 모든 쌍별 상호 작용을 평가할 수 있습니다.
2.1 선형 회귀 모형
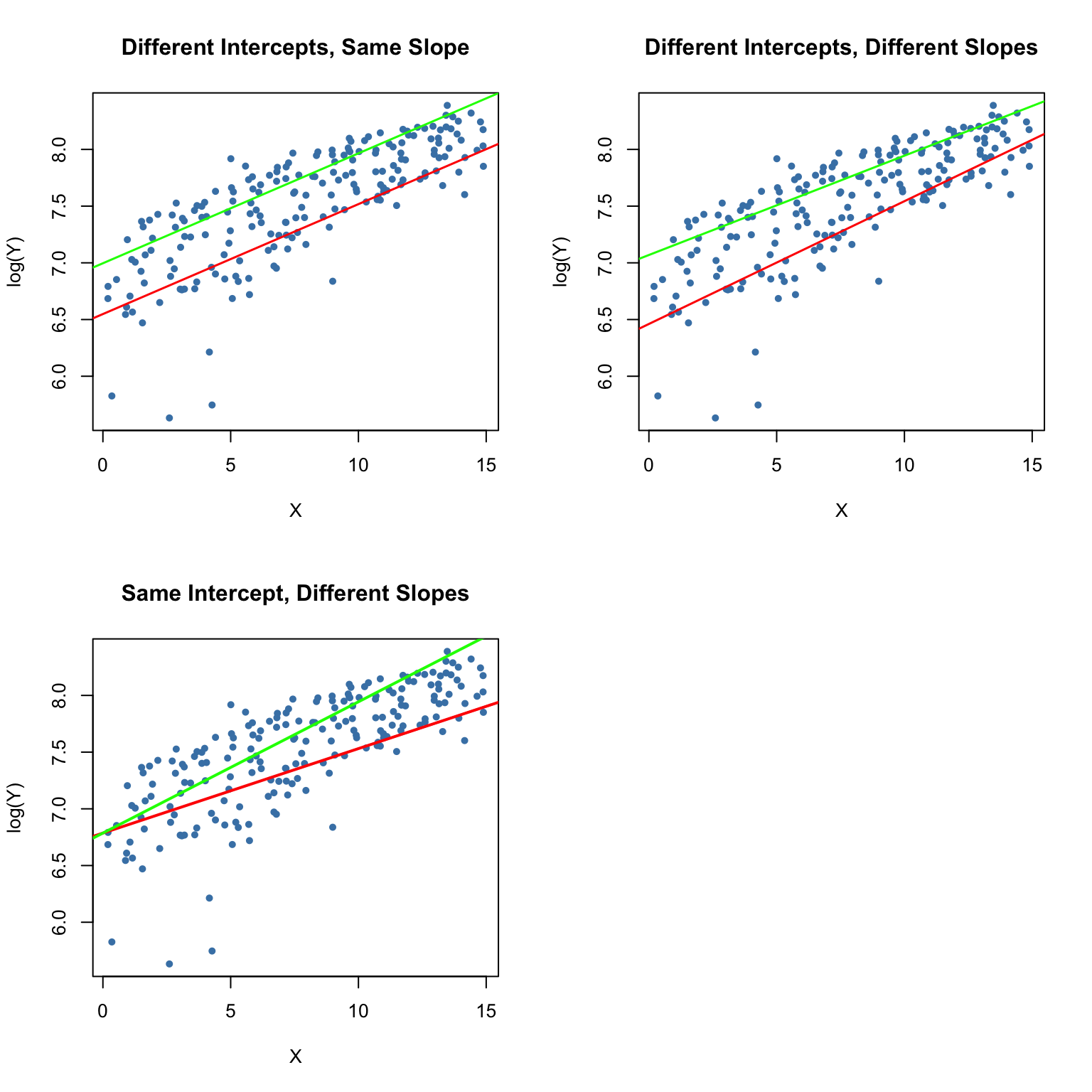
중요한 교호 작용 항을 스크리닝하는 전통적인 방법은 중첩 된 통계 모델을 사용하는 것입니다. 예측 변수
x1 및 x2와 상호 작용이 있는 모델과 그렇지 않은 모델은 다음과 같습니다.
$$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + error$$
$$y = \beta_0 + \beta_1x_1 + \beta_2x_2 + \beta_3x_1x_2 + error$$
선형 회귀 분석의 경우 모형을 비교하는 데 사용되는 목적 함수는 통계적 우도입니다 (이 경우 잔차 오류)
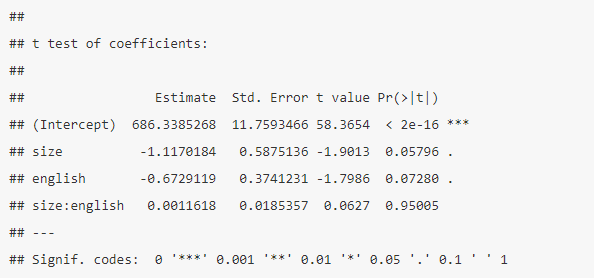
3. 완전한 열거가 실제로 불가능할 때의 접근법
3.1 지도 원리 및 2 단계 모델링
2 단계 모델링 접근법에서 예측 변수가 반응의 변동을 설명하는 능력은 상호 작용 효과를 직접 설명하지 않는 모델을 사용하여 평가됩니다. 이러한 모형의 예는 선형 또는 로지스틱 회귀입니다. 중요한 예측 변수가 확인되면 이 모형의 잔차가 계산됩니다. 이 잔차에는 개별 예측 변수 자체가 설명 할 수 없는 정보가 포함되어 있습니다. 설명 할 수 없는 변동은 임의 측정 오류로 인한 것이며, 사용 가능하거나 측정되지 않은 예측 변수 또는 모델에없는 관측 된 예측 변수 간의 상호 작용으로 인한 것일 수도 있습니다. 보다 구체적으로, 관측 된 데이터가 방정식에서 생성되었다고 가정합니다.
$$y = \beta_0 + \beta_1x_1 + error*$$
$$error* = \beta_2x_2 + \beta_3x_1x_2 + error$$
error*을 설명하기 위해 x2와 상호작용을 넣고 어느정도를 설명하는 지 확인하는 방법이 있습니다.
3.2 트리 모형
지금까지 논의 된 방법은 적당한 수의 예측 변수를 가진 데이터에 대한 상호 작용을 드러내는 데 효과적 일 수 있습니다. 그러나 이러한 접근 방식은 예측 변수 수가 증가함에 따라 실질적인 효과를 잃습니다. 재귀 분할 또는 재귀 분할 모델의 앙상블과 같은 트리 기반 방법은 많은 예측 변수를 사용하여 데이터를 효율적으로 모델링 할 수 있습니다. 또한, 트리 기반 방법은 변수 사이의 잠재적 인 상호 작용을 밝혀내는 것으로 나타났습니다 (Breiman et al. 1984 ).
Friedman and Popescu ( 2008 ) 는 앙상블을 사용하여 상호 작용을 식별하기위한 이론적 부분 의존성 개념 (Friedman 2001 ) 을 기반으로 한 접근법을 제시합니다 . 요컨대,이 접근법은 두 개 이상의 예측 변수의 결합 효과와 모형의 각 예측 변수의 개별 효과를 비교합니다. 개별 예측 변수가 다른 예측 변수와 상호 작용하지 않으면 관절 효과와 개별 효과의 차이가 0에 가까워집니다. 그러나 개별 예측 변수와 하나 이상의 예측 변수간에 상호 작용이 있으면 차이가 0보다 큽니다.
상호 작용을 식별하는 세 번째 실용적인 방법은 예측 변수 중요 정보와 계층 구조, 희소성 및 유전 원칙을 사용합니다. 간단히 말해 예측 변수 간의 상호 작용이 중요한 경우 트리 기반 방법은 여러 예측 트리에서 이러한 예측 변수를 여러 번 사용하여 응답과의 관계를 파악합니다. 이러한 예측 변수는 0이 아닌 중요도가 높은 값을 갖습니다. 그런 다음 가장 중요한 예측 변수 간의 쌍별 상호 작용을 만들어 반응 예측과의 관련성을 평가할 수 있습니다. 이것은 기본 학습자가 트리 기반 모델이라는 점을 제외하고 2 단계 모델링 접근 방식과 매우 유사합니다.
참고자료
'EDA Study > 머신러닝' 카테고리의 다른 글
| Dataprep.eda : Accelerate your EDA (EDA 자동화 패키지) (3) | 2020.04.15 |
|---|---|
| 임베딩 기법(Embedding) (0) | 2020.03.28 |
| Feature selection using target permutation (Null Importance) (0) | 2019.09.11 |
| Attn: Illustrated Attention (0) | 2019.09.11 |
| ADSP 3과목 정리내용 - 5장: 정형 데이터 마이닝 (0) | 2019.03.02 |



