ADSP 3과목 정리내용 - 5장: 정형 데이터 마이닝

교재 : 데이터 분석 준 전문가 Adsp 2017

 

데이터 분석 

• 1장. 데이터 분석 개요
• 2장. R프로그래밍 기초
• 3장. 데이터 마트
• 4장. 통계 분석
• 5장 정형 데이터 마이닝

 

 

4장. 통계 분석 

- PCA 주성분 분석

: 기존의 상관성이 높은 변수들을 요약, 축소하여 선형결합으로 만드는 방법!!! = 차원을 축소하는 방법.

 

출처 : http://geog.uoregon.edu/GeogR/topics/pca.html

 

• Proportion of Variance : 변수가 설명하는 정도. 주성분1은 95.5%를 설명함. 
• Cumulative Proportion : 위의 Proportion of Variance의 누적값.  

 

위와는 다른 예시지만 Component Number의 수에 따라 변동성을 보여 줌.

 

 

위의 테이블은 2개의 변수 long과 diag가 주성분1과 2에 기여하는 가중치를 보여주는 부분. 

• Comp.1 = 0.707*long + 0.707*diag
• Comp.2 = -0.707*long + 0.707*diag

 

 

 

5장. 정형 데이터 마이닝

• 제 1절 : 데이터 마이닝의 개요 

 

데이터 마이닝 : 데이터로부터 의미있는 정보를 찾아내는 방법 , 통계 분석 : 가설이나 거정에 따른 분석이나 검증을 하는 과정. 

 

Supervised Data Prediction	Unsupervised Data Prediction
특징 : Y(target)을 아는 상태로 예측.	특징 : Y(target)을 모르는 상태로 사용.
의사결정나무 (Decision Tree)  인공신경망 (NN)  일반화 선형 모델 (GLM)   KNN	OLAP  연관성 규칙발견  군집분석  SOM
예 : 회귀분석, 판별분석, 신경망, 의사결정나무	예 : 연속규칙, 연관규칙, 클러스터링

 

Supervised 같은 경우는 Y값에 대한 것을 알고 싶을 때, Unsupervised 같은 경우는 X들의 관계를 알고 싶을 때 사용하는 방법. 

 

분석방법이 많이 나오는데 방법, 장점, 단점 위주로 공부하기!!!

- 제 2절 - 1 : 의사결정나무 분석 

 

1) 분류 분석(Classification) vs 예측 분석(Prediction or Regression)

- 공통점 : X를 이용해 Y를 맞추는 방법 

- 차이점 : 분류 분석 - 범주형( 개 vs 고양이 ), 예측 분석 - 연속형 ( 주가 예측 )

 

예) 타이타닉 - 성별, 나이, 자녀 수, 자매 수, 티켓 비용 등 개인정보와 탑승 정보를 통해서 생존 여부를 분류하는 문제. 

 

출처 : https://ko.m.wikipedia.org/wiki/%EA%B2%B0%EC%A0%95_%ED%8A%B8%EB%A6%AC_%ED%95%99%EC%8A%B5%EB%B2%95

   

 

위와 같이 분류에도 사용하고 예측에도 사용하는 방법임. 

 

장점 : 해석력이 좋음, 정확도가 높음. 

단점 : 오버피팅의 위험도가 높음. 

-> 위의 예를 보면 남자 -> 나이가 9.5살 이상 -> 자매 수가 2.5명 이상 에서 끊기는 데, 여기에 자식 수 + 티켓 비 + 탑승 위치 등 여러 정보가 추가 되어서 가지가 확장 될 수 있음. 

 

그래서 이를 해결하기 위해 꼭 나오는 내용 중 하나가 '가지치기(Pruning)' 이라는 표현이 나옴. 너무 가지가 확장 되면 의도적으로 가지를 자르는 행위. 

 

본격적으로 Decision Tree의 알고리즘의 순서를 살펴보면 

1. Y를 예측 할 중요한 변수를 찾음 (위에서는 성별 -> 나이 -> 자매 수 이런 순으로 결정 됨) 

2. Cutoff value 값을 정함. 나이에서는 9.5의 값을 의미

3. 가지치기 

 

여기서 드는 의문점은 1에서 중요한 변수를 어떻게 찾느냐 부터 시작 됨. 이를 위해 우리는 불순도라는 것을 측정하게 됨. 이 불순도라는것이 지니지수, 엔트로피 지수. 

 

의사결정나무 알고리즘 

1. CART : 분류 및 예측 모두 가능한 방법

2. C4.5, C5.0 : 분류에만 사용 

3. CHAID : 카이제곱 통게량 사용 

 

- 제 2절 - 2 : 앙상블 분석

앙상블 : 여러가지 예측모형들을 만든 후 조합하여 하나의 최종 예측모형을 만드는 방법 

 

장점 : 성능이 많이 좋아짐. 오버피팅도 방지 됨. 

단점 : 해석력이 많이 떨어짐. 모델이 무거워짐. 

 

1. 배깅(bagging : bootstrap aggregating)

2. 부스팅(boosting)

 

1. 배깅(bagging : bootstrap aggregating) - Amelia, Mice가 이와 같은 방법. 

 

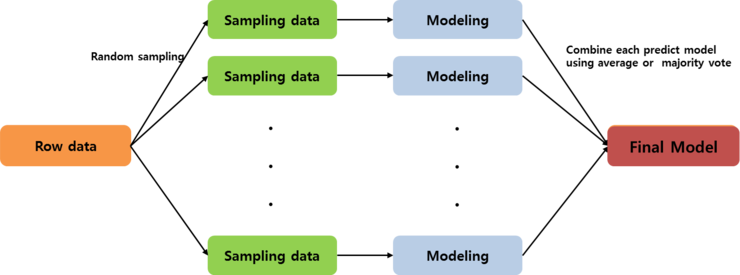
(출처 : https://m.blog.naver.com/muzzincys/220201299384)

 

예 : Random Forest. - Modeling으로 Decision Tree를 여러개 만든 다음에 평균내는 방법. 

 

2. 부스팅(Boosting) - Xgboost , LightGBM , Catboost, Adaboost 

 

예 : Adaboost - 

 

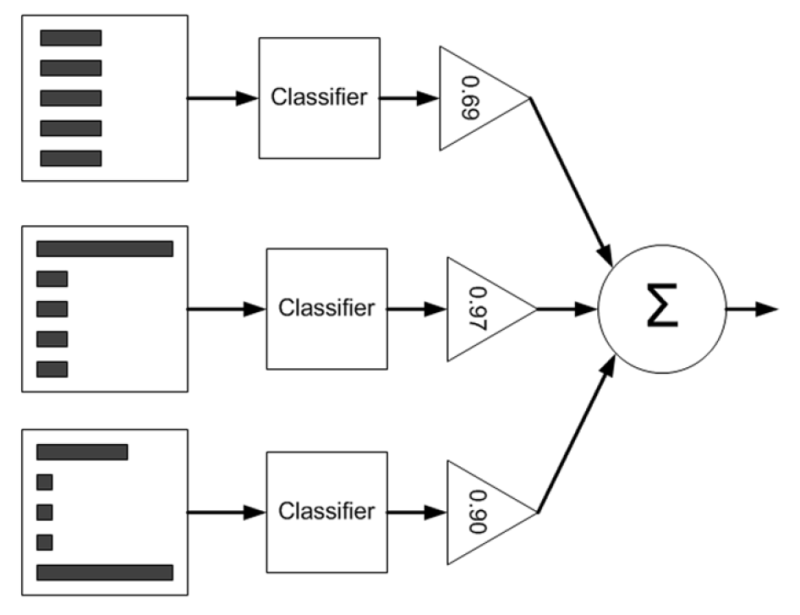
위의 두가지 모델 사이의 차이점 ?!

- Bagging은 순서가 없음!!!! 한번에 여러가지의 샘플링 된 데이터를 만들고 모델을 만든다음에 평균 냄. 

- Boosting은 순서가 있음!!!! 처음 모델에서 못 맞춘 부분을 다음 모델이 잘 맞추도록 학습시키는 방법!!!

 

성과분석 <- 개인적으로 외우고 갔으면 좋겠음. 

 

출처 ; http://cdn.differencebetween.net/wp-content/uploads/2018/07/Difference-Between-Sensitivity-and-Specificity.jpeg

 

예측한게 맞으면 True, 예측한게 틀리면 False 

실제 값이 양수면 Positive , 실제 값이 음수면 Negative 

Sensitivity = TP / ( TP + FN ) : 민감도 Positive로 예측해서 Positive 맞힌 비율 

Specificity = TN / ( TP + TN ) : 특이도 Negative로 예측해서 Negative 맞힌 비율 

 

 

출처 : https://i2.wp.com/www.theanalysisfactor.com/wp-content/uploads/2018/12/roc_curve.png?ssl=1

 

1 - 특이도 : 1 - TN / ( FP + TN ) = FP / ( FP + TN ) , Negative로 예측했는데 실제로는 Postive인 비율 

 

- 제 2절 - 3 : 신경망 분석, 로지스틱 회귀분석 

신경망 분석 (ANN, DNN) 

 

출처 : https://upload.wikimedia.org/wikipedia/commons/thumb/4/46/Colored_neural_network.svg/300px-Colored_neural_network.svg.png

 

입력층 - 히든층 - 아웃풋 

 

x1에 들어오는 입력 값 : x1  --- 가중치 값 ---> h1에 들어오는 입력 값 : x1wx1 + x2wx1 + x3wx1

y1에 들어오는 입력 값 : h1wh1 + h2wh1+ h3wh1+ h4wh1  --- 활성화 함수(전이 함수) ---> y1의 출력 값 

 

활성화 함수의 종류 

1. 시그모이드

2. Relu 

3. 계단 

4. 선형 

 

고려사항 

- 연속형 변수 : 정규화 

- 범주형 변수 : 동일한 범위 갖도록 조정 

 

문제 : 은닉층이 커짐에 따라 과대적합의 문제가, 적어짐에 따라 과소적합의 문제가 발생하므로 잘 조정해야 함.

 

로지스틱 회귀분석 (Logistic Regression)

반응변수(Y)가 범주형인 경우에 적용되는 회귀분석모형이다. - 범주형 변수를 사용하므로 Classification문제 임. 

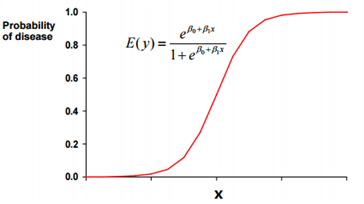
- 제 3절 - 군집분석 

클러스터링이라고도 표현하며 유사한 데이터를 찾아서 같은 군집으로 분류하는 방법. 

 

*거리의 정의* - 저 시험떄 나왔던 문제. 

연속형 : 유클리드 거리, 표준화 거리, 마할라노비스, 체비셰프, 맨하탄, 캔버라, 민코우스키 

범주형 : 자카드 거리

 

계층적 군집방법 : n개의 군집으로 시작해 점차 군집의 갯수를 줄여가는 방법  

 장점 : K의 갯수를 몰라도 괜찮음 

 

 

1) 최단연결법 (single linkage, nearest neighbor)

 

 

 

2) 최장연결법 

 

 

3) 평균연결법

 

 

4) 와드연결법 -> 나올 것이라고는 생각하지 않음. 

 

군집내의 편차들의 제곱합을 고려한 방법 : 처음에 de로 묶은 후에 아래처럼 유사도를 측정해서 가장 작은 것을 집어넣음. 

 

(출처 : https://rfriend.tistory.com/m/227)

 

비계층적 군집방법 : 

1) k - means

 

출처 : https://www.google.com/search?q=k-means+%EC%98%88%EC%8B%9C&prmd=ivn&source=lnms&tbm=isch&sa=X&ved=2ahUKEwi5yp2XoePgAhUOyosBHZo2D48Q_AUoAXoECAwQAQ#imgrc=MiRaL_RWsVksBM

 

 

a -> b로 넘어갈 때 Random하게 k개의 중심을 정함. 

b -. c로 넘어갈 때 설정한 두개의 중심에 가까운 곳에 군집을 설정. (위의 중심과 가까운 곳은 빨강, 아래의 중심과 가까운 곳은 파랑)

c -> d로 넘어갈 때, c에서 새로 중심을 설정. 

d -> e로 넘어갈 때, 새로 설정 된 중심에 따라 가까운 곳으로 할당. 

e -> f로 넘어갈 때, 중심을 다시 정하고 반복. 

 

장점 : 알고리즘이 단순하며, 빠르게 수행 , 많은 양의 데이터를 다룰 수 있음 

단점 : 군집의 갯수 k와 가중치 w, 거리 d를 정의하기 어려움. 결과해석이 어려움. 잡음이나 이상치에 영향을 많이 받음. convex한 군집에 대해 적용하면 성능이 떨어짐. (아래의 사진에서 딱 보면 알것임.)

 

출처 :  https://t1.daumcdn.net/cfile/tistory/99B35B3359DB7BBE23

 

 

 

혼합 분포 군집 (mixture distribution clustering)

*모형 기반*의 군집 방법이며 데이터가 K개의 모수적 모형의 가중 합으로 표현 되었을 때 사용되는 방법. 

- 아래의 분포 혹은 위의 그림에서 1~2번째 줄 같은 경우가 *   모형 기반*

 

출처 :  https://ratsgo.github.io/machine%20learning/2017/05/01/SOM/  

 

 

SOM ( Self - Organizing Map ) 

 

출처 : https://ratsgo.github.io/machine%20learning/2017/05/01/SOM/ <- 들어가서 설명 확인 

부족하면 아래의 https://untitledtblog.tistory.com/5 여기 추가로 설명. 

 

 

 

제 4절 : 연관분석 

예) 기저귀를 사는 고객이 맥주를 같이 사는 경향을 보인다. 

 

1) 연관분석(Association Analysis)

- 흔히 장바구니분석 또는 서열분석이라고 불린다. 

 

2) 연관규칙의 개념 

- 장바구니에 무엇이 같이 들어 있는지에 대한 분석

- A를 산 다음에 B를 산다. 

 

3) 연관분석의 측도 <- 문제 나오기 딱 좋은 부분. 

- 지지도 : A와 B가 동시에 포함된 거래수 / 전체 거래수 

- 신뢰도 A : A와 B가 동시에 포함된 거래수 / A를 포함하는 거래수

- 향상도 : A와 B가 동시에 포함된 거래수 / A를 포함하는 거래수 X B를 포함하는 거래수

 

4) 연관규칙의 절차 

- 최소지지도보다 큰 집합만을 대상으로 높은 지지도를 갖는 품목 집합을 찾음. 

- 최소 지지도 결정 -> 품목 중 최소 지지도를 넘는 품목 분류 -> 2가지 품목 집합 생성 -> 반복적으로 수행 

( 예시 : https://ratsgo.github.io/machine%20learning/2017/04/08/apriori/)

 

 

상대도수는 자기가 포함 된 거래를 모두 계산. 확률은 전체 거래수에서 계산한 부분. 

 

장점 : 1. 결과를 쉽게 이해할 수 있음 2. 목적변수가 없어도 활용할 수 있음

 

단점 : 1. 계산양이 큼. 2. 품목이 세분화되면 의미가 없어짐.