| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Object Detection
- 알고리즘
- 파이썬
- hackerrank
- 나는 리뷰어다
- Semantic Segmentation
- 추천시스템
- 한빛미디어
- 입문
- 엘리스
- 코딩테스트
- Image Segmentation
- Recsys-KR
- TEAM EDA
- 큐
- 나는리뷰어다
- Segmentation
- DFS
- TEAM-EDA
- Python
- Machine Learning Advanced
- DilatedNet
- 3줄 논문
- MySQL
- 협업필터링
- 튜토리얼
- 스택
- eda
- 프로그래머스
- pytorch
- Today
- Total
TEAM EDA
[Machine Learning Advanced] 5강. 머신러닝 강의 - 기본 ML 모델 (KNN) 본문
[Machine Learning Advanced] 5강. 머신러닝 강의 - 기본 ML 모델 (KNN)
김현우 2023. 8. 15. 22:07
이번 강의에서는 머신러닝 모델 중에서 Non-Linear 모델 중 두번째인 KNN(K-Nearest Neighborhood) 방법에 대해 알아보도록 하겠습니다.
KNN 모델이란 무엇이고 왜 알아야 하는 것일까요?
KNN (최근접 이웃법)은 비선형모델의 하나로서 Tree 방식과는 다르게, 가장 가까운 K개의 데이터를 보고 해당 데이터가 속할 그룹을 판단하는 방법입니다. 아래의 예시에서는 삼각형에 대한 분류를 K=1일때는 보라색 사각형으로, K=3일때는 핑크색 원으로 분류한 것을 볼 수 있습니다.

이러한 KNN은 모델을 별도로 구축하지 않는다는 의미로 게으른 모델(Lazy model)이라고 부르기도하고, memory-based learning, instance based model 등 여러 표현으로 부르기도 합니다. KNN의 경우 예측 및 분류에서도 쓰이지만 여러군데에서 유용하게 쓰이는 모습을 보입니다. 예를들어, 결측치를 채우거나 이상치를 대체할때 KNN을 사용하기도 하고 추천시스템 분야에서 KNN을 아직도 많이 이용합니다. 실제로 카카오 아레나 3차 경진대회에서 KNN 기반의 방법론이 좋은 성능을 거두기도 하였습니다.
KNN 은 어떻게 작동할까요?
KNN은 학습이라는 개념이 없습니다. 대신에 "새로운 데이터가 들어왔을때 가장 가까운 거리의 K개의 데이터 보고 판단"하겠다만 남습니다. 이때, 중요한 부분은 거리와 K의 정의입니다. 머신러닝에서 거리에 대한 정의는 다양합니다. 대표적으로,
유클리드 거리 (L2 Distance)
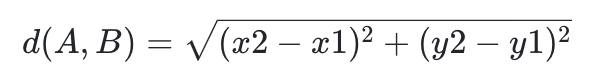
맨해튼 거리 (L1 Distance)
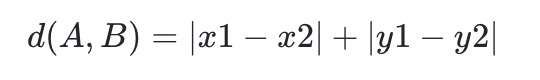
2개의 측정방식이 유명합니다. 해당 방식은 다른 표현으로는 L2, L1 거리라고도 부르며 선형회귀에서 잠깐 봤던 Ridge (L2), Lasso (L1)와 같은 개념이라고 보시면 될 것 같습니다. 그렇다면, 이러한 K와 거리의 정의에 따라 KNN은 어떻게 작동을 할까요?
[K에 따른 KNN결과]
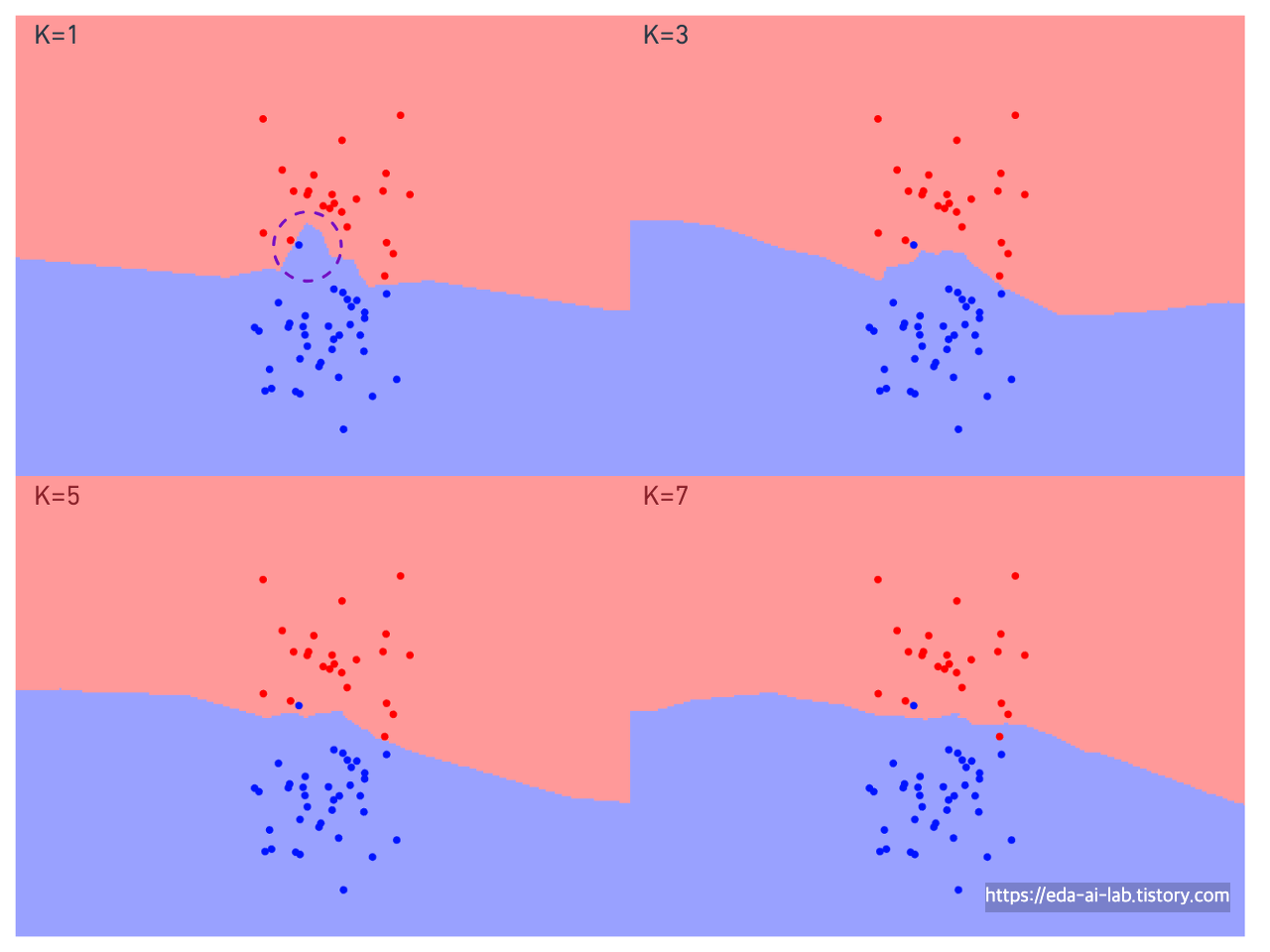
위의 그래프는 K값에 따라서 파란색 클래스로 분류되는 영역과 빨간색 클래스로 분류되는 영역을 색칠한 그래프입니다. K가 커짐에 따라서 점차 경계선이 완만해지는 모습을 보이고, 특히 K가 가장작은 1일때는 보라색 원을 친 영역처럼 특정 하나의 포인트에의해 해당 주변이 빨간색이 아닌 파란색 클래스로 분류되는 것을 볼 수 있습니다. (전반적인 추세로 보면 주변이 빨간색이 더 많아 빨간색 클래스일 가능성이 더 높은데도 말입니다). 그렇기에, KNN의 특징 중 하나가 K가 작을때는 과적합 될 가능성이 높다는 점입니다.

그리고, K가 작을때는 이상치에 영향도 많이 받는데 간단하게 임의의 점 2개를 추가함에 따라 파란색 영역이 극단적으로 넓어짐과 동시에, 빨간색 부분이라고 생각되는 부분의 대부분이 파란색으로 넘어간 것을 볼 수 있습니다.
[Distance 정의에 따른 KNN결과]
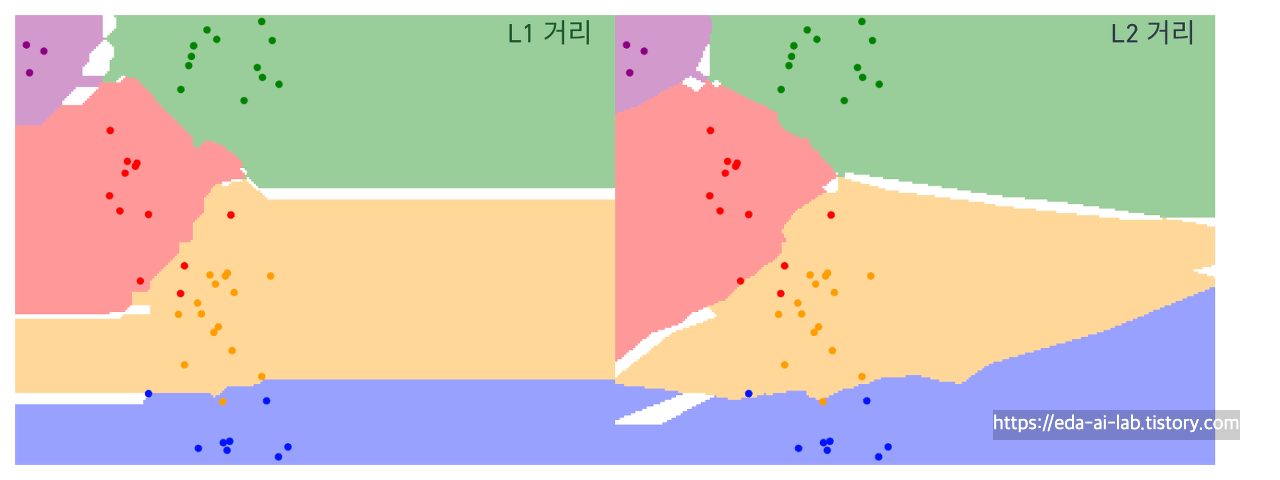
L1과 L2 거리방식에 따른 영역의 차이는 두가지가 있습니다. 첫째, L1은 절대값을 사용하다보니 직교형태의 경계면이 만들어지는 모습을 보이고 L2는 좀 더 스무스한 경계면이 이어지는 모습을 보입니다. 둘째, L2의 경우 제곱을 사용하다 보니 포인트들이 모인 부분과 거리가 먼 영역에 대해 행사하는 힘이 더 강해지는 것 같습니다. 예를들어, L2에서 파란색영역이 오른쪽위로 상승하는 모습을 볼 수 있습니다.
KNN을 사용시에 주의해야할 점은 무엇이 있을까요?
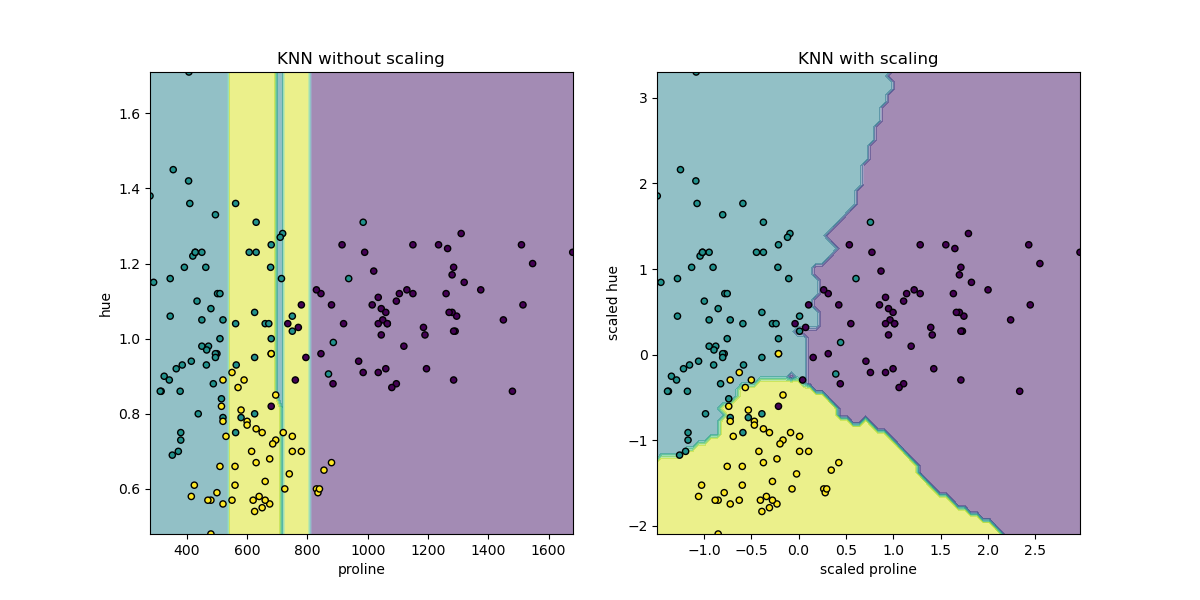
첫번째로는 변수들간의 스케일입니다. 예를들어, x1은 0~10 사이의 값을 가지고 x2는 0~1000000000 사이의 값을 가지면 어떻게 될까요? 거리를 계산하게 되면 x2의 영향이 크다보니 x1의 영향은 거의 없어질 것입니다. 위의 그림에서는 hue와 proline의 스케일이 다르다보니 KNN의 계산이 proline에 따라 종속되는것을 볼 수 있습니다. 따라서, 이러한 변수들간의 스케일 차이로 인한 영향을 없애주기 위해 Normalization의 방법을 고려해볼 수 있습니다.
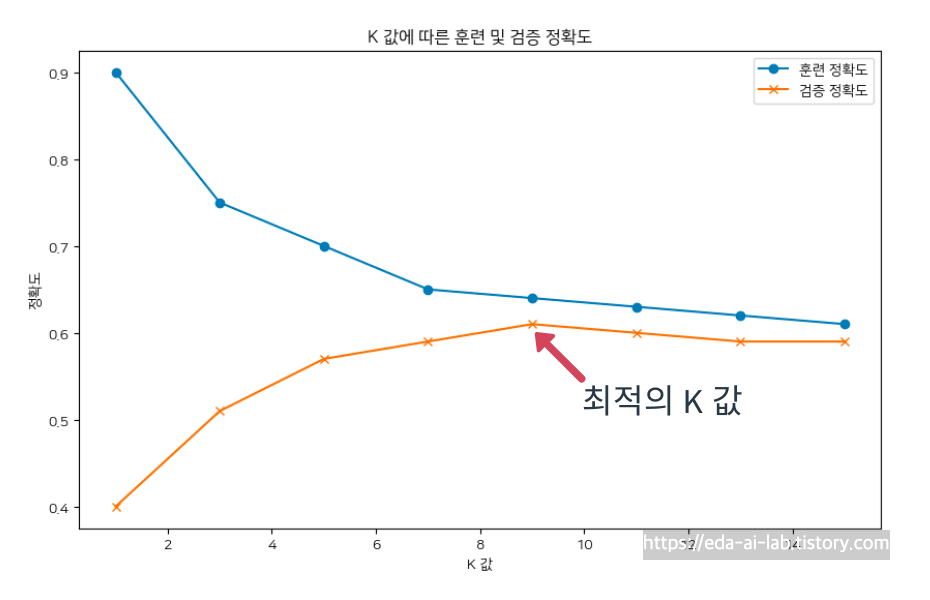
두번째로는 K의 선택입니다. 너무 작은 K는 Overfitting을 너무 큰 K는 Underfitting을 유발합니다. 그로인해, 적절한 K의 선택이 필요합니다. 이러한 부분은 일반적으로는 검증 셋을 만들어서 실험을 통해 결정합니다. (참고로 distance 방법 또한 검증 셋을 통해서 정하게 됩니다)
KNN의 장점과 단점은 무엇이 있을까요?
장점:
1. 간단하고 직관적인 알고리즘
2. 비모수적 방법: KNN은 데이터의 분포에 대한 가정이 필요하지 않음
3. 분류 뿐만 아니라 회귀에도 적용 가능
4. 새로운 관측치가 추가될 때마다 KNN이 쉽게 적용 가능
단점:
1. 대용량의 데이터셋에서 KNN은 모든 데이터 포인트 간의 거리를 계산해야 하므로 계산 비용이 매우 높음
2. 모든 학습 데이터를 메모리에 저장해야 하므로 저장 공간이 크게 필요
3. 하이퍼파라미터의 선택: K의 값, 거리 측정 방법 등 KNN의 성능에 영향을 미치는 하이퍼파라미터를 적절하게 선택
4. 불균형 데이터 문제: 한 클래스의 데이터 포인트가 다른 클래스보다 훨씬 많은 경우, 그 클래스가 지배적으로 되어 다른 클래스의 데이터 포인트가 잘못 분류될 수 있음
KNN의 응용은 무엇이 있을까요?
[결측치 채우기]
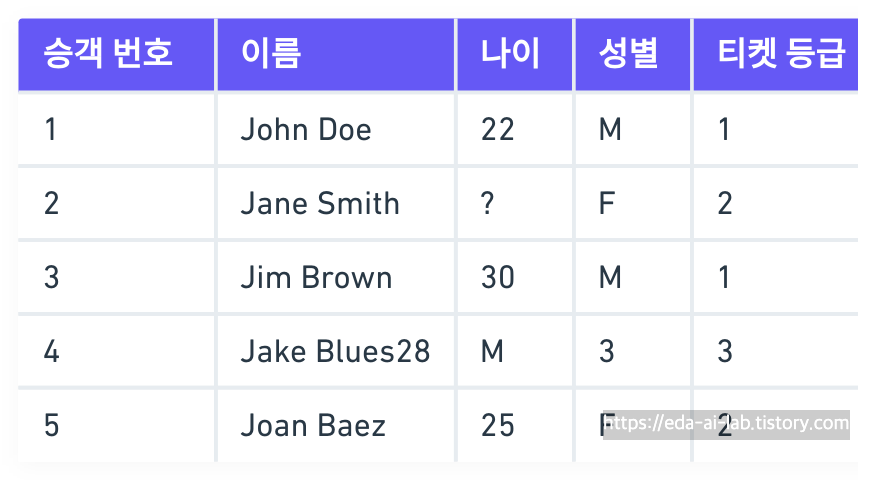
KNN은 결측치를 채우는데 활용가능합니다. Jane Smith의 나이가 누락되었다고 가정하면, 가장 가까운 이웃들의 나이를 참고하여 결측치를 채울 수 있습니다. 예를 들어, K=2로 설정하면 가장 가까운 두 이웃을 찾아 그들의 나이의 평균값으로 Jane Smith의 나이를 예측합니다. 위의 예시에서는 ‘티켓 등급‘과 ‘성별‘을 특성으로 사용한다고 가정하면 Jane Smith와 가장 유사한 이웃은 John Doe와 Joan Baez입니다. 이 경우, 두 이웃의 나이 평균은 (22 + 25) / 2 = 23.5입니다. 따라서 Jane Smith의 예상 나이는 23.5으로 결측치를 채울 수 있습니다.
참고자료
https://ratsgo.github.io/machine%20learning/2017/04/17/KNN/
'EDA Study > Machine Learning Advanced' 카테고리의 다른 글
| [Machine Learning Advanced] 8강. 머신러닝 강의 - 캐글에서 활용되는 알아두면 좋은 팁 (Tips) (5) | 2023.08.26 |
|---|---|
| [Machine Learning Advanced] 2강. 머신러닝 강의 - 데이터 전처리 (연속형 변수) (0) | 2023.08.17 |
| [Machine Learning Advanced] 3강. 머신러닝 강의 - 파생 변수 만들기 (4) | 2023.08.14 |
| [Machine Learning Advanced] 5강. 머신러닝 강의 - 기본 ML 모델 (의사결정 나무) (5) | 2023.08.12 |
| [Machine Learning Advanced] 5강. 머신러닝 강의 - 기본 ML 모델 (선형 모델) (1) | 2023.08.11 |




