| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 엘리스
- 알고리즘
- Image Segmentation
- 나는리뷰어다
- 큐
- 코딩테스트
- pytorch
- 튜토리얼
- 프로그래머스
- Recsys-KR
- Machine Learning Advanced
- 파이썬
- Python
- 협업필터링
- hackerrank
- Segmentation
- DFS
- 3줄 논문
- 나는 리뷰어다
- TEAM EDA
- 한빛미디어
- Semantic Segmentation
- eda
- DilatedNet
- 입문
- Object Detection
- TEAM-EDA
- MySQL
- 추천시스템
- 스택
- Today
- Total
TEAM EDA
linear regression (선형회귀분석) with R 본문
linear regression (선형회귀분석) with R
김현우 2019. 9. 10. 12:13Note: 이번 내용은 Jaeyoon Han님의 자료를 저희 스터디원이 진행 한 발표내용을 중심으로 추가적인 discussion을 정리했습니다.회귀분석의 개념과 추가적인 내용 및 파이썬 코드에 관한 부분은 아래의 링크를 참고하시기 바랍니다. 개인적으로 이해한 내용으로 작성한 자료니 틀린 부분이나 모르는 부분은 댓글로 남겨주시기 바랍니다!!!
링크 : http://blog.naver.com/choco_9966/221254266558
목차
1. 지도학습/비지도학습/강화학습의 개념
2. 선형회귀법(Linear Regression)
3. 선형회귀법 실습 with R
1. 지도학습/비지도학습/강화학습의 개념
| 지도학습 (Supervised Learning) | 목적값을 알고있는 data를 가지고 기계학습 알고리즘을 진행. |
| 비지도학습 (Unsupervised Learning) | 목적값을 모르는 data를 가지고 기계학습 알고리즘을 진행. |
| 강화학습 (Reinforcement Learning) | 위와는 다르게 잘하면 상을주고 못하면 벌을 주는 형식으로 기계학습 알고리즘을 진행. |
2. 선형회귀법(Linear Regression)
Y = b0 + b1*x1 + b2*x2 + ··· + bp*xp 와 같이 x라는 독립변수(independent variable)에 대해서 y라는 종속변수(dependent variable)의 관계를 선형으로 구하는 것을 선형회귀법이라 합니다. Y = b0 + b1*x1 같이 하나의 독립변수(x가 한개)인 경우를 단순 선형 회귀(Simple Linear Regression)이라 하고 위 빨간색의 식처럼 독립변수(x)가 여러개인경우를 다중 선형 회귀(Multiple Linear Regression)이라 합니다.
간단하게 시각적으로 이해하면 아래 그림과 같습니다. 빨간색의 점(실제 y값)들 사이의 관계를 파란색 선(회귀선/예측값)을 그어서 확인하는게 저희의 목표입니다.


선형회귀를 위한 수학적 증명은 아래 링크에 정리해 두겠습니다.
링크 : http://blog.naver.com/choco_9966/221254266558
3. 선형회귀법 실습 with R
(1) 가정
● 종속변수와 독립변수 사이에 선형성 이 성립한다.
●독립변수는 확실하게 측정된 값 으로, 확률적으로 변하는 값이 아니다.
●오차항의 평균은 0이며, 분산은 시그마제곱 인 정규 분포를 따른다.
●서로 다른 오차항은 독립 이다.
●독립변수간 다중공선성 (multicollinearity)이 적어야 한다
참고 : https://m.blog.naver.com/archiku/50115462325
가정에 대한 내용을 좀 더 자세하게 설명해줍니다.
일단 이러한 가정은 선형회귀법에서 최소제곱법(OLS)를 사용해서 나오는 부분이고, 이러한 부분이 이용되는 분야는 뒤에 다시 설명하겠습니다.
(2) 실습자료 1
data(cars)
head(cars)
#r에 내장된 cars 데이터를 가지고 speed와 dist간의 선형회귀분석을 진행하겠습니다.
> head(cars)
speed dist
1 4 2
2 4 10
3 7 4
4 7 22
5 8 16
6 9 10
# 목표 dist ≈ β0 + β1 * speed.
model <- lm(dist ~ speed, data = cars)
# lm은 R에 내장된 함수로 linear regression을 불러들이는 함수이고, cars라는 data에서 y값으로는 dist를 x값으로는 speed를 넣으라는 명령어 입니다.,
> model
Call:
lm(formula = dist ~ speed, data = cars)
Coefficients:
(Intercept) speed
-17.579 3.932
# 결론 dist ≈−17.579+3.932×speed.
# 이제 추가적으로 더 자세한 내용을 보기 위해서 summary라는 명령어와 plot이라는 명령어를 입력해 보겠습니다.
> summary(model)
Call:
lm(formula = dist ~ speed, data = cars)
# 실제 y와 예측한 y사이의 차이를 의미합니다.
Residuals:
Min 1Q Median 3Q Max
-29.069 -9.525 -2.272 9.215 43.201
# 여기서 Estimate를 통해 베타를 확인하고 뒤의 p-value를 통해 베타(계수)가 유의미한지 확인합니다.
# 둘다 0.05미만으로 유의미하고 signif. codes는 중요한 정도에 따라 오른쪽에서부터 왼쪽으로 중요도가 늘어나고 기호가 바뀝니다.
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -17.5791 6.7584 -2.601 0.0123 *
speed 3.9324 0.4155 9.464 1.49e-12 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 15.38 on 48 degrees of freedom
# R-squared는 설명의 정도를 알려주는 공식인데, 왼쪽의 R-squared는 row가 증가함에따라 값이 증가해서 Adjusted R-squared를 사용합니다
# 0.64는 전체데이터의 64%를 설명한다는 의미.
Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438
# 마지막 p-value는 과연 이러한 회귀분석모델 자체가 유의미한지를 확인하는것으로 유의수준5%에서 의미가 있는것을 확인할 수 있습니다.
F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12par(mfrow = c(2, 2))
plot(model)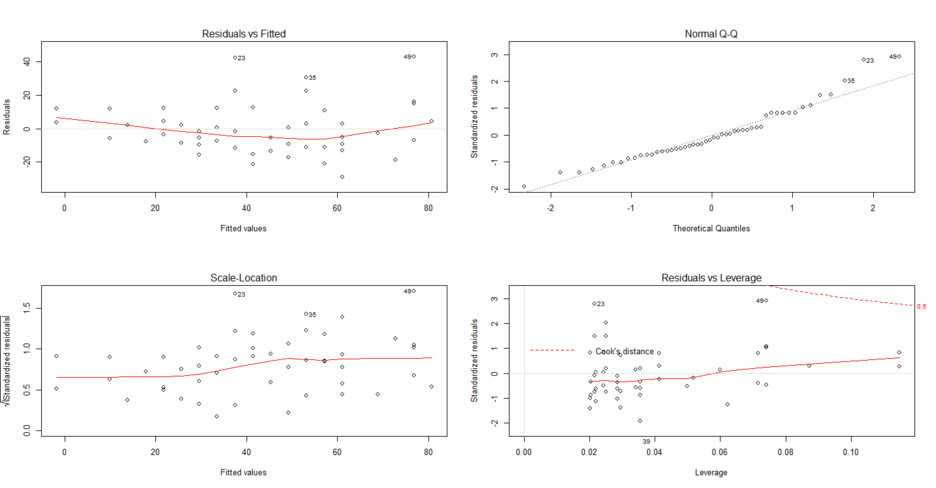
왼쪽위에부터 시계방향으로 차근차근 설명해 보겠습니다.
1번째 그림
첫 번째 그림은 잔차(residuals)와 모델에서 예측된 Y값(fitted value, Yhat) 사이의 그래프입니다. 우리가 최소제곱법에서 예측할 때 가능하면 잔차의 크기가 작을 뿐 아니라 분포가 한 곳에 몰리지 않고 일정해야 모델이 좋은 것이라고 할 수 있습니다. 따라서 관측값들이 가능하면 골고루 분포해야 하며 그 평균인 붉은 색 실선이 평행해야 하는데, 이 정도면 어느 정도 통과하는 것 같다고 평가할 수 있지만 완벽하지는 않습니다.
위와 같이 말하는 이유는 잔차와 fitted value 사이의 아무런 관계가 없다는것을 보여주기 위함입니다.
한마디로 위의 가정에서 오차항의 평균이 0이고 분산이 시그마제곱인 정규 분포를 따른다는 점을 보여줍니다.
2번째 그림
두번쨰 는 normal Q-Q 플롯으로 흔히 Q-Q 플롯으로 불리는 것입니다. 이는 정규분포에 따르는 Quantile과 표본의 Quantile의 비교를 보여주는 것으로 가능한 직선으로 일치해야 모델이 적합한 것입니다.
3번째 그림
세 번째는 표준화 잔차의 루트를 씌운 값과 회귀식에서 예측값(적합값)의 분포를 보여줍니다. 가능하면 값들이 한 곳에 몰리지 않고 골고루 분포할 뿐 아니라 잔차의 값이 작을수록 회귀 모형이 좋은 것입니다.
4번째 그림
마지막 그림은 지렛값이라고 하는 레버리지 (Leverage) 값을 보여주는 그림입니다. 지렛값은 시소를 타고 있는 사람을 생각해 보면 이해가 쉽습니다. 만약 여러 사람이 탄 시소에서 중앙에서 가장 먼 거리에 누군가 앉게되면 같은 무게라도 시소 기울기에 큰 영향을 주게 됩니다. 지렛값은 이렇게 하나의 관측치인데 예측 모형에서 많이 벗어나 있어 전체 모형의 회귀계수에 큰 영향을 주는 값을 의미합니다. 여기에서는 20번 관측치가 가장 크게 벗어난 것으로 보입니다.
지렛값의 크기를 구하는 가장 중요한 방법으로 쿡의 거리 (Cook's distance)가 있습니다. 관측값들이 회귀 모형에 적합해서 큰 영향을 주지 않으면 쿡의 거리는 작은 반면 적합하지 않아서 많이 영향을 주면 쿡의 거리가 길어집니다. 여기서는 관측치 49이 가장 먼 거리에 있으며 0.5 이상으로 나옵니다. 쿡의 거리가 1 이상이면 매우 큰 것이고 0.5도 무시할 수 없는 수준입니다.
출처 : https://blog.naver.com/jjy0501/221206148507 // 굉장히 참고 많이했습니다.
●독립변수간 다중공선성 (multicollinearity)이 적어야 한다
library(car)
vif <- vif(lm(dist ~ speed, data = cars))
> vif <- vif(lm(dist ~ speed, data = cars))
Error in vif.default(lm(dist ~ speed, data = cars)) :
model contains fewer than 2 terms
# 지금 내용은 단순선형회귀분석이여서 (독립변수가 한개여서) 확인을 못하지만, 다중선형회귀분석에서는 이를 통해
# 다중공선성이 10이하인것을 확인해야 합니다.@@@
'TEAM EDA > EDA 1기 ( 2018.03.01 ~ 2018.09.16 )' 카테고리의 다른 글
| kaggle - Rossmann Store sales Prediction (1) (0) | 2019.09.10 |
|---|---|
| Decision Tree (의사결정나무) (0) | 2019.09.10 |
| 결측치 처리 (Missing Value) (3) | 2018.11.12 |
| EDA (Exploratory Data Analysis) 탐색적 데이터 분석 (8) | 2018.11.12 |
| TEAM-EDA 1기 활동 내역 (0) | 2018.11.12 |



