| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- Semantic Segmentation
- Segmentation
- 알고리즘
- Object Detection
- 코딩테스트
- Machine Learning Advanced
- pytorch
- 협업필터링
- DilatedNet
- Recsys-KR
- 한빛미디어
- TEAM-EDA
- 프로그래머스
- MySQL
- 나는 리뷰어다
- 튜토리얼
- 나는리뷰어다
- Image Segmentation
- eda
- 파이썬
- 큐
- 입문
- 추천시스템
- 3줄 논문
- hackerrank
- 엘리스
- DFS
- Python
- 스택
- TEAM EDA
- Today
- Total
TEAM EDA
[파이토치로 시작하는 딥러닝 기초] 1.6 Softmax Classification 본문
이번 글에서는 PyTorch로 Softmax Classification을 하는 방법에 대해서 배워보도록 하겠습니다. 이번 글은 EDWITH에서 진행하는 파이토치로 시작하는 딥러닝 기초를 토대로 작성하였습니다.
목차
- Softmax
- Cross Entropy
- Low-level Implementation
- High-level Implementation
1. Softmax
Discrete Probability Distribution
- 정의 : 이산적인 확률 분포
- 예 : 주사위를 던질 경우에 1에서부터 6 중 하나에 분포하게 됨.

이산적인 확률분포를 바탕으로 우리는 Neural Net, Machine Learning을 수행합니다. 예를 들어, 가위바위보를 예측하는 프로그램을 만든다고 생각했을 때, 철수가 가위를 낸 이후 주먹을 낼 확률은 얼마? P(주먹 | 가위) 와 같은 값들을 궁금하게 됩니다. 그리고 P(주먹 | 가위), P(가위 | 가위), P(보 | 가위) 이 세 가지를 알게 되면, 철수가 가위 이후에 무엇을 낼지 알게 되고 이길 수 있게 됩니다. 우리는 이러한 확률들을 모델들로 근사하려고 하는데, 이를 softmax를 이용해서 하게 됩니다.
softmax의 수식은 아래와 같으며 직관적으로는 각 클래스의 값을 확률로 바꿔주는 함수입니다.

z = torch.FloatTensor([1, 2, 3])
hypothesis = F.softmax(z, dim=0)
print(hypothesis)
2. Cross Entropy (Low-level)
Cross Entropy는 두개의 확률분포가 주어졌을 때, 둘이 얼마나 비슷한지를 나타내는 수치라고 할 수 있습니다. ratsgo님의 블로그에서는 손실 함수로 음의 로그우도를 사용하는 이유를 확률론적인 접근과 정보이론적인 접근으로 나누고, 확률론적인 접근에서는 "최대 우도 추정"을 위해서입니다. 최대 우도 추정의 관점에서는 로그를 씌어도 argmax의 결과는 바뀌지 않고 아래의 식을 최대로 하는 세타만을 계산하게 됩니다.
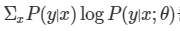
정보이론적인 접근에서는 두 확률분포 사이의 차이를 계산하는데 사용한다고 생각할 수 있습니다. 즉, 우리가 가진 데이터의 분포 P(y|x)와 모델이 예측한 결과의 분포 P(y|x; 세타) 사이의 차이를 계산하게 됩니다. 이게 성립하는 이유는 P(y|x)는 1과 0을 가지는 관측치이기 때문입니다. 만일 P(y|x)가 1일 때, 학습이 잘 되지 않아서 logP(y|x; 세타)가 log0이게 되면 그 값은 무한대로 치솟게 되고 반대로 0일 때도 똑같습니다.
이렇게 되면 우도의 곱이 최대인 모델을 찾는 것(최대우도함수)은 로그 우도의 기댓값이 최대인 모델을 찾는 것과 같으며(확률에 로그를 씌운 결과, 로그를 씌우기에 곱이 합으로 바뀌어서 기댓값이 됨), 이는 학습 데이터의 분포와 모델이 예측한 결과의 분포 사이의 차이, 즉 크로스 엔트로피를 최소화하는 것과 동치입니다.
출처 : 딥러닝 모델의 손실함수 ratsgo's blog
3. Low-level Implementation
x_train = [[1, 2, 1, 1],
[2, 1, 3, 2],
[3, 1, 3, 4],
[4, 1, 5, 5],
[1, 7, 5, 5],
[1, 2, 5, 6],
[1, 6, 6, 6],
[1, 7, 7, 7]]
y_train = [2, 2, 2, 1, 1, 1, 0, 0]
x_train = torch.FloatTensor(x_train)
y_train = torch.LongTensor(y_train)
# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산 (1)
# z에 softmax를 씌워서, 각각의 row의 합이 1이 되도록
hypothesis = F.softmax(x_train.matmul(W) + b, dim=1) # or .mm or @
y_one_hot = torch.zeros_like(hypothesis) # 값을 모두 0으로 반환
y_one_hot.scatter_(1, y_train.unsqueeze(1), 1) # y의 index자리에 1을 넣기
cost = (y_one_hot * -torch.log(F.softmax(hypothesis, dim=1))).sum(dim=1).mean()
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))# 모델 초기화
W = torch.zeros((4, 3), requires_grad=True)
b = torch.zeros(1, requires_grad=True)
# optimizer 설정
optimizer = optim.SGD([W, b], lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# Cost 계산 (2)
z = x_train.matmul(W) + b # or .mm or @
cost = F.cross_entropy(z, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 100번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))4. High-level Implementation
class SoftmaxClassifierModel(nn.Module):
def __init__(self):
super().__init__()
self.linear = nn.Linear(4, 3) # Output이 3!
def forward(self, x):
return self.linear(x)
model = SoftmaxClassifierModel()
# optimizer 설정
optimizer = optim.SGD(model.parameters(), lr=0.1)
nb_epochs = 1000
for epoch in range(nb_epochs + 1):
# H(x) 계산
prediction = model(x_train)
# cost 계산
cost = F.cross_entropy(prediction, y_train)
# cost로 H(x) 개선
optimizer.zero_grad()
cost.backward()
optimizer.step()
# 20번마다 로그 출력
if epoch % 100 == 0:
print('Epoch {:4d}/{} Cost: {:.6f}'.format(
epoch, nb_epochs, cost.item()
))'EDA Study > PyTorch' 카테고리의 다른 글
| [파이토치로 시작하는 딥러닝 기초] 2.3 ReLU (0) | 2020.03.20 |
|---|---|
| [파이토치로 시작하는 딥러닝 기초] 2.1~2 Perceptron, Multi Layer Perceptron (0) | 2020.03.20 |
| [파이토치로 시작하는 딥러닝 기초] 1.5 Logistic Regression (1) | 2020.03.20 |
| [파이토치로 시작하는 딥러닝 기초] 1.4.2 Loading Data (0) | 2020.03.19 |
| [파이토치로 시작하는 딥러닝 기초] 1.2~4 Linear Regression (0) | 2020.03.19 |




