| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 한빛미디어
- 스택
- 나는 리뷰어다
- Object Detection
- 파이썬
- Segmentation
- eda
- 협업필터링
- TEAM EDA
- Recsys-KR
- Machine Learning Advanced
- 큐
- Python
- Image Segmentation
- hackerrank
- 엘리스
- 나는리뷰어다
- MySQL
- 3줄 논문
- pytorch
- Semantic Segmentation
- DFS
- 튜토리얼
- TEAM-EDA
- 추천시스템
- 코딩테스트
- 프로그래머스
- 입문
- 알고리즘
- DilatedNet
- Today
- Total
TEAM EDA
Lecture 3: Word Window Classification,Neural Networks, and Matrix Calculus 본문
Lecture 3: Word Window Classification,Neural Networks, and Matrix Calculus
김현우 2019. 4. 19. 12:09이번 Lecture3에서는 지난Lecture2(https://eda-ai-lab.tistory.com/122)에 이어서 Word window Classification과 NN에 대해 알아보도록 하겠습니다. 지난번과 마찬가지로 파리의 언어학도블로그의 글을 토대로 내용을 추가하였습니다.

일반적으로 우리는 training dataset을 i=1부터 N까지 xi라는 inputs과 yi라는 output(label or class)에 대해 가지고 있습니다. nlp에서는 xi는 단어나 문장, 문서를 의미하고 yi는 classes일수도 words나 다른 것들일 수도 있습니다.

위의 데이터를 ML/ Deep Learning 방법으로 분류의 과정을 거치게 됩니다. 분류는 아래의 그림처럼 비슷한 비슷한 Output끼리 모이도록 경계를 긋는 것을 의미합니다. 전통적인 ML접근에서는 softmax/ logistic regression을 이용해서 output의 class를 구분할 decision boundary (hyperplane)를 결정하는 것을 의미합니다.

주어진 Method 부분은 input이 주어졌을 때, Output이 나올 확률을 나타낸 것입니다.

이를 보다 자세하게 살펴보도록 하겠습니다. 먼저 softmax에 대한 개념부터 잡고 넘어가겠습니다. softmax는 lectures01에서 아래와 같이 정의하였습니다.

xi가 들어오면 이를 pi로 바꾸는 것을 의미합니다. 그리고 분류하고 싶은 클래스의 수 만큼 확률값을 구성하며, 모든 클래스의 확률값을 더하면 1이 된다는 특징을 가지고 있습니다.
두가지 Step으로 Softmax Classifier에 대해 보면, 모든 클래스 c에 대해서 선형결합으로 이루어진 fy를 만들고 각각의 클래스에 대해 이를 계산하고 0~1로 정규화 하면 됩니다.
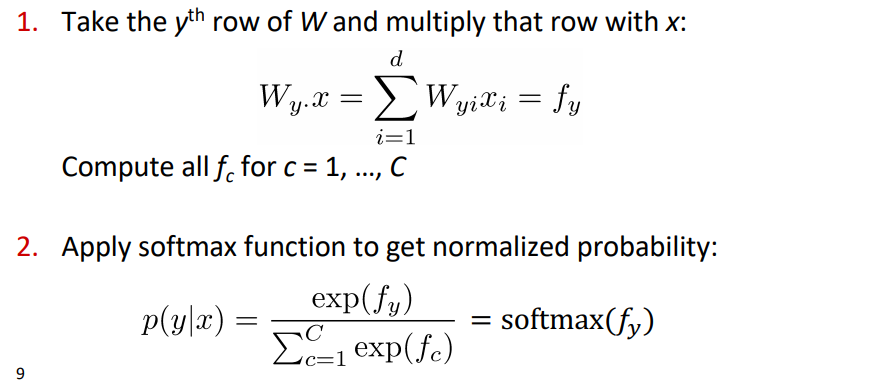
이제 이 값을 학습할 때, 올바르게 y값을 예측하도록 확률을 극대화 하든가 negative한 값을 최소화하도록 학습을 하게 됩니다.

참고로 cross entropy loss/error에 대해서 알아보도록 하겠습니다. cross entropy는 정보이론으로부터 나온 개념입니다. 실제 확률 분포를 p라고 하고, 예측한 확률 분포를 q라고 하였을 때, cross entropy는 아래와 같이 계산됩니다.

p = [0,...,0,1,0,...,0] 의 값을 가지고 q = [ 0.01,...,0.02, 0.8,0.01...,0]의 값을 가지기 때문에, 잘못 분류한 확률들은 0으로 사라지고 실제 클래스의 negative log probability 값만을 가지게 됩니다. 위의 식을 전체 데이터 셋으로 확장하면 아래의 공식과 같습니다. i = 1 부터 N까지의 평균으로 loss부분을 업데이트 해주었습니다.

하지만 단순한 Softmax ( logistic regression ) 하나만으로는 좋은 성능을 낼 수 없습니다. 그 이유는 위의 그림처럼 class를 구분하는 boundary가 선형의 형태이기 때문입니다. 이를 해결하기 위해서 비선형적인 방법을 도입하는데 그게 바로 Neural Network입니다.

NLP에서 딥러닝은 아래와 같이 가중치 W와 word vectors X에 대해 학습을 진행합니다.
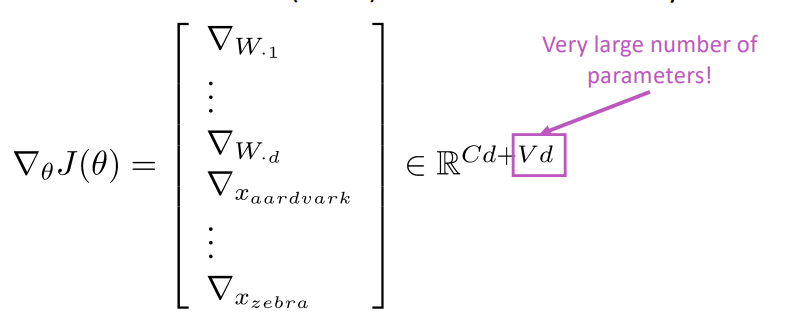

개체명 인식(Named entity recognition)은 인명, 지명 등 고유명사를 분류하는 방법론입니다. 가능한 목적들로는
- 문서의 특정 항목에 대한 언급 추적
- 질문 답변의 경우 답변은 일반적으로 이름이 지정된 항목입니다.
- 많은 필요로하는 정보들은 지정된 이름들과 연관이 있습니다.
- 동일한 기술들이 다른 slot-filling classifications으로 확장될 수 있습니다.
하지만 NER은 매우 힘든 기술입니다. 그 이유는

- entity(개체)의 경계를 정하기 어렵습니다. 위의 첫번째 entity를 First National Bank로 or National Bank로 잡을지 부터 이슈가 생깁니다.
- 그리고 개체인지 아닌지 알기가 어렵습니다. 위에서 Future School이 의미하는게 school을 "Future School" 이라고 부르는지 혹은 미래의 학교라는 의미인지 알 수 없습니다.
- 모르는 entity(개체)에 대해 class를 알 기 힘듭니다. 아래의 "Zig Ziglar"가 사람임에도 class를 알 기 힘듭니다.
- Entity class는 모호하고 문맥에 의존합니다.



일반적으로, single words의 분류는 잘 하지 않고 문맥상에서 애매모호하게 일어나는 것들이 흥미로운 주제입니다. 예를들어, auto-antonyms (자동-반의어)의 경우입니다.
- "To sanction" can mean "to permit" or "to punish”
- "To seed" can mean "to place seeds" or "to remove seeds"
위의 두가지 예문처럼 동일한 표현이 반대의 의미로 인식되는 경우라든지, 아래의 예시처럼 개체가 애매모호한 연결성을 가질 때 입니다. (France의 paris인지 Paris Hilton인지 전부다 연결 될 수 있으니 그 중에서 무엇을 의미하는지 모른다는 것 같습니다.)
- Paris à Paris, France vs. Paris Hilton vs. Paris, Texas
- Hathaway à Berkshire Hathaway vs. Anne Hathaway

window classification의 기본적인 생각은 중심 단어와 주변 단어들 (context)를 함께 분류문제에 활용하는 방법입니다.
간단한 방법으로는 context내 단어를 분류하기위해 window안의 word vectors를 평균내고, 이 average vector를 분류하는 것입니다. (하지만 이럴경우, position 정보를 잃어버리는 단점이 있습니다.)
Example : "Paris"를 window length 2로 분류하기 위해서, 먼저 주변단어와 중심단어를 합칠 필요가 있습니다. 그러면 합쳐진 벡터의 크기는 5d의 크기를 가지게 됩니다.

이제 Collobert& Weston (2008, 2011) 의 방법을 이용해서 Binary classification with unnormalized scores를 하게 됩니다. 위의 Xwindow가 주어졌을 때, 우리는 center word Paris가 지역인지 아닌지 궁금합니다. word2vec에서는 corpus내 모든 위치에 대해서 학습을 진행하였지만, 이번에는 high score을 가지는 위치에 대해서만 학습을 진행합니다.
(E.g., the positions that have an actual NER location in their center are "true" positions and get a high score - 중심단어가 중앙에 오는 상황에서만 학습한다는 의미같습니다. - 불확실ㅠㅠ )
Example : Not all museums in Paris are amazing.
예를들어, 위와 같은 문장이 있습니다. Paris를 중심단어로 하는 Xwindow는 museums in Paris are amazing이 될 것입니다. 이를 true window라고 하고, 그렇지 않은 windows들을 corrupt하다고 표현합니다. 에를들어, 아래의 예시처럼 중심단어가 구체적인 NER 지역이 아닌 경우입니다.
Example : Not all museums in Paris
활성화 함수 a는 input word vectors의 non-linear interactions를 담당한다.

Neural Network의 손실함수 (max-margin loss = hinge loss)
일반적으로 softmax를 사용할 경우 값을 확률 비율로 변경했기 때문에 비율간의 차이를 계산하는 Cross-entropy를 사용하는게 일반적이다. 하지만, 위에서 score함수를 직접 정했으므로 여기에서는 이에 걸맞는 max-margin loss(hinge loss)를 이용한다. max margin loss는 SVM에서 많이 사용되었는데, 그 의미가 정답과 오답 사이의 거리를 최대로 만들어주는 margin을 찾는 것이다. 쉽게 말하면 주어진 input X에 대하여 정답 class아 오답 class 간의 차이를 max로 만들어주는 손실함수이다. 하지만 여기에서는 정답과 오답의 차이가 k이상일 경우 loss를 0으로 만든다. (한마디로 정답으로 본다) 아래 그림에서는 k=1로 정하였고 이게 일반적이다.

Neural Network,의 Back Propagation
우리는 앞서 작성한 max-margin 손실함수를 통해 손실값을 구했다. 이제 이 손실값에 각 파라미터 W, U, b, X가 손실값에 얼마나 많은 기여를 했는지 알아보고 해당 기여도에 따라 각 parameter 값을 조정해보자. 일단 손실값이 발생했을 때를 가정해서 업데이트를 해보자. 편미분J/ 편미분U를 해야하는데, 사실상 J= Sc값에 의해 좌지우지 되고, 편미분J/편미분s = - 편미분J/편미분Sc = -1이기 때문에 손실값 J를 s라고 봐도 무방하다. 따라서, 에러에 대한 U의 기여도를 알기위해 손실값 U로 편미분하면 편미분s/편미분u = a = Wx + b가 된다.

Parameter W에 대한 Backpropagation



참고자료
'강의 내용 정리 > CS224N' 카테고리의 다른 글
| Lecture 2: Word Vectors and Word Senses (2) | 2019.04.14 |
|---|---|
| Lecture 1 – Introduction and Word Vectors (0) | 2019.04.13 |


