Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 튜토리얼
- Segmentation
- 프로그래머스
- TEAM-EDA
- hackerrank
- Object Detection
- pytorch
- 스택
- 파이썬
- Recsys-KR
- 큐
- Semantic Segmentation
- 협업필터링
- 3줄 논문
- 나는 리뷰어다
- 입문
- TEAM EDA
- 엘리스
- Machine Learning Advanced
- 알고리즘
- 나는리뷰어다
- Image Segmentation
- 한빛미디어
- Python
- DilatedNet
- 추천시스템
- DFS
- eda
- MySQL
- 코딩테스트
Archives
- Today
- Total
TEAM EDA
[엘리스] 최대 공통 부분 수열 본문
최대 공통 부분 수열
두 개의 문자열 s1, s2 가 주어질 때, 공통 부분 수열이란, s1과 s2가 공통으로 갖는 부분 수열을 일컫는다. 예를 들어, s1 = “Television”, s2 = "Telephone"이라고 하면, s1과 s2의 공통 부분 수열이 될 수 있는 문자열은 “T”, “To”, “Teln” 등이 있다.
최대 공통 부분 수열이란, 공통 부분 수열 중에서 그 길이가 최대인 것을 일컫는다. 예를 들어, s1 = “Television”, s2 = "Telephone"이라고 하면, 그 최대 공통 부분 수열은 "Teleon"으로써, 그 길이는 6이다.
두 개의 문자열이 주어질 때, 최대 공통 부분 수열의 길이를 구하는 프로그램을 작성하시오.
입력
첫 번째 줄에 문자열 s1, 두 번째 줄에 문자열 s2가 주어진다. 각 길이는 1000을 넘지 않는다.
출력
최대 공통 부분 수열의 길이를 출력한다.
입력 예시
Television
Telephone출력 예시
6풀이
- $LCS(X_i, Y_j)$의 경우 3가지 케이스로 나눔
- i or i가 0이면 0을 가짐
- $x_i == y_j$이면 $LCS(X_{i-1}, Y_{j-1}) + 1$
- $x_i != y_j$이면 $max(LCS(X_{i-1}, Y_{j}), LCS(X_{i}, Y_{j-1}))$
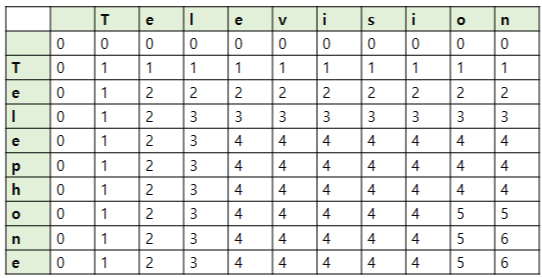
- 문자를 하나씩 늘려가면서, 가장 최장의 길이를 계산함
import sys
def LCS(s1, s2) :
'''
문자열 s1, s2의 최대 공통 부분 수열의 길이를 반환하는 함수를 작성하세요.
# 링크 : https://mygumi.tistory.com/126
'''
s1_len = len(s1)
s2_len = len(s2)
data = [[0 for i in range(s2_len+1)] for j in range(s1_len+1)]
for i in range(1,s1_len+1) :
for j in range(1,s2_len+1) :
if s1[i-1] == s2[j-1] :
data[i][j] = data[i-1][j-1] + 1
else :
data[i][j] = max(data[i-1][j], data[i][j-1])
return data[s1_len][s2_len]
def main():
'''
이 부분은 수정하지 마세요.
'''
s1 = input()
s2 = input()
print(LCS(s1, s2))
if __name__ == "__main__":
main()
출처 : 엘리스 아카데미, https://academy.elice.io/learn
'EDA Study > 알고리즘' 카테고리의 다른 글
| [엘리스] 팰린드롬 (0) | 2020.03.29 |
|---|---|
| [엘리스] 두 문자열 사이의 거리 (0) | 2020.03.29 |
| [엘리스] N-Queen (0) | 2020.03.29 |
| [엘리스] 가로수 (0) | 2020.03.29 |
| [알고리즘] 최대공약수 구하기 (0) | 2020.03.28 |




