| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 나는 리뷰어다
- 프로그래머스
- Object Detection
- Semantic Segmentation
- 파이썬
- Machine Learning Advanced
- Python
- 코딩테스트
- 추천시스템
- DilatedNet
- DFS
- eda
- 입문
- TEAM EDA
- 3줄 논문
- 한빛미디어
- Image Segmentation
- MySQL
- 나는리뷰어다
- 알고리즘
- pytorch
- 스택
- Segmentation
- 튜토리얼
- 엘리스
- hackerrank
- TEAM-EDA
- 협업필터링
- Recsys-KR
- 큐
- Today
- Total
TEAM EDA
알고리즘 트레이닝 : 프로그래밍 대회 입문 가이드 본문
본 포스터는 인사이트에서 <알고리즘 트레이닝 : 프로그래밍 대회 입문 가이드>책을 지원받아 작성한 리뷰 포스터입니다. 먼저 저는 비전공자이고 책의 코드인 C++은 전혀 모르는 상황이고 프로그래밍은 2년 정도 알고리즘은 작년에 3달 정도 공부한 학생입니다.

먼저 책을 읽고 난 느낌부터 말하자면, (1) C++을 전혀 모르시는 분 (2) 공부 의지가 약하신 분한테는 추천드리지 않고 (1) 프로그래밍 대회를 나가고 싶은 분 (2) C++ 코드의 성능을 높이고 싶은 분들한테는 적극적으로 추천합니다. 그 이유는 아래에 내용 부분에서 설명해 드리도록 하겠습니다.
1. 책 소개
<알고리즘 트레이닝 : 프로그래밍 대회 입문 가이드>는 다른 책들과는 다르게 경진 프로그래밍 대회에 참여해서 성적을 거둘 수 있도록 하는 가이드 책입니다. 300페이지에 걸쳐서 (1) 효율적 코드 작성 (2) 기초 알고리즘 (3) 고급 알고리즘 (4) 경진 프로그래밍과 관련된 수학 4가지에 대해 중점적으로 다룹니다. 출판사의 설명에 따르면 "이 책은 따라 해보기 쉽게 구성되어 있기 때문에, 알고리즘을 배우고 프로그래밍 대회를 연습하고 싶은 학생들에게 훌륭한 참고서가 될 것이다. 몇몇 알고리즘 설계 기법은 온라인 게시판이나 블로그 글에만 간단히 소개되는 등 제대로 정리된 자료가 부족하여 상위권 경진 프로그래머들 사이에서만 주로 공유되는데, 이 책은 그런 '민간전승' 기법들을 다루고 있는 점도 눈에 띈다. 활용하기 좋은 프로그래밍 기법, 최신 트렌드 및 대회에서 유용한 트릭까지, 다루는 주제의 폭이 넓고 그 난이도도 다양해서 초보자와 경험자 모두에게 적합한 책이다."라고 나와있습니다. 자세한 목차는 아래의 부록에 작성했습니다.
2. 책 내용
내용의 구성은 다른책들처럼 이론 + 예제문제로 구성되어있습니다. 예를 들어서 최대 부분 배열 합이라는 문제가 주어졌을 때, 아래의 인용구처럼 풀이방법과 코드를 알려줍니다.
내용의 구성은 다른 책들처럼 이론 + 예제 문제로 구성되어있습니다. 예를 들어서 최대 부분 배열 합이라는 문제가 주어졌을 때, 아래의 인용구처럼 풀이 방법과 코드를 알려줍니다.
> 3.2.1 최대 부분 배열 합
우리가 살펴볼 첫 번째 문제는 배열에 수 n 개가 들어있을 때 최대 부분 배열 합(maximum subarray sum)을 구하는 문제이다. 즉, 배열에서 연속해 있는 값들을 택하여 그 합을 최대로 만드는 것이다. 이 문제는 배열에 음수가 포함되어 있을 때 좀 더 재밌어진다. 예를 들어 그림 3.1에 예제 배열과 합이 최대인 부분 배열이 나와 있다.

O(n3) 시간 풀이
이 문제를 푸는 직관적인 방법은 가능한 모든 부분 배열을 하나씩 살펴보고, 그 부분 배열의 합을 구한 후, 최대 합을 관리해 나가는 것이다. 다음 코드는 이 알고리즘을 구현한 것이다.
int best = 0;
for (int a = 0; a <n; a++) {
for( int b = a; b < n; b++){
int sum = 0;
for (int k =a; k <= b; k++){
sum += array[k];
}
best = max(best, sum); }
}
cout << best << "\n";변수 a와 b는 부분 배열의 첫 번째 위치와 마지막 위치를 나타내고, 부분 배열의 합을 계산하여 변수 sum에 저장한다. 변수 best에는 답을 구하는 과정에서 찾은 최대 합을 기록한다. 이 알고리즘의 시간 복잡도는 O(n3)인데, 입력을 한 번씩 살펴보는 반복문이 3중으로 중첩되어 있기 때문이다.
위의 코드 및 설명을 보면 알겠지만 기본적으로 C++ 코드를 알고 있다는 가정하에 설명이 진행됩니다. 그리고 코드에 대한 설명이 모든 것을 알려주는 것은 아니고 핵심만 딱 짚어서 설명해주는 스타일입니다. 그렇기에 설명이 이해가 안 가면 여러 번 다시 보면서 공부해야 합니다. 하지만, 이 책을 읽으면서 가장 맘에 든 점 중 하나는 문제에 대한 풀이를 다양하게 제공합니다. 위의 코드는 시간 복잡도 O(n3)에 대해 설명한 코드인데, 바로 다음 페이지에는 O(n2)로 푸는 방법, O(n)으로 푸는 방법까지 설명이 되어 있습니다. 코딩 문제를 풀다 보면 주어진 문제를 다양한 시각으로 접근할 수 있어야 하는데 그러한 부분에서는 굉장히 만족한 부분이었습니다.
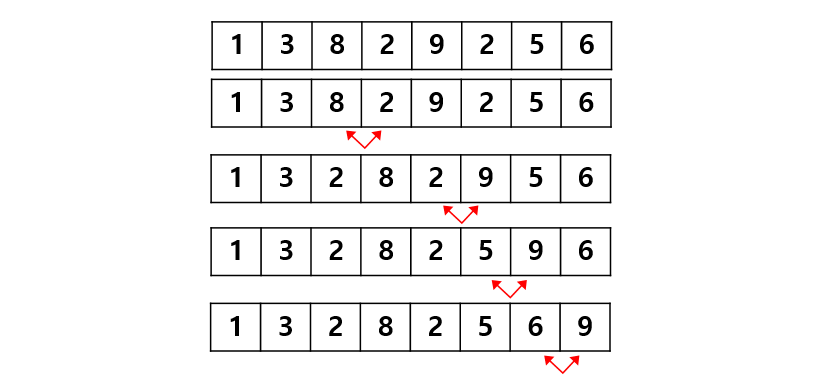
아래는 정렬의 방법 중 하나인 버블 정렬에 대해서 설명한 예시에서 나온 그림입니다.
> 4.1.1 버블 정렬
문제 풀이에서 느꼈던 불친절함과는 다르게 이론에서 친절하다고 느꼈던 점은 대부분의 설명에 그림이 들어가 있다는 점입니다. 그렇기에 시각적으로 진행과정을 살펴보기에는 좋았습니다.
그리고 책을 읽으면서 다른 책들과 가장 다르다고 생각한 부분이 두 가지가 있습니다.
첫째, 수학입니다. 책에서는 알고리즘을 이해하고 활용해야 하는데 필요한 수학에 대해 설명하고, 이를 어떻게 사용하는지에 대해 설명해줍니다.

둘째, 고급 알고리즘입니다.
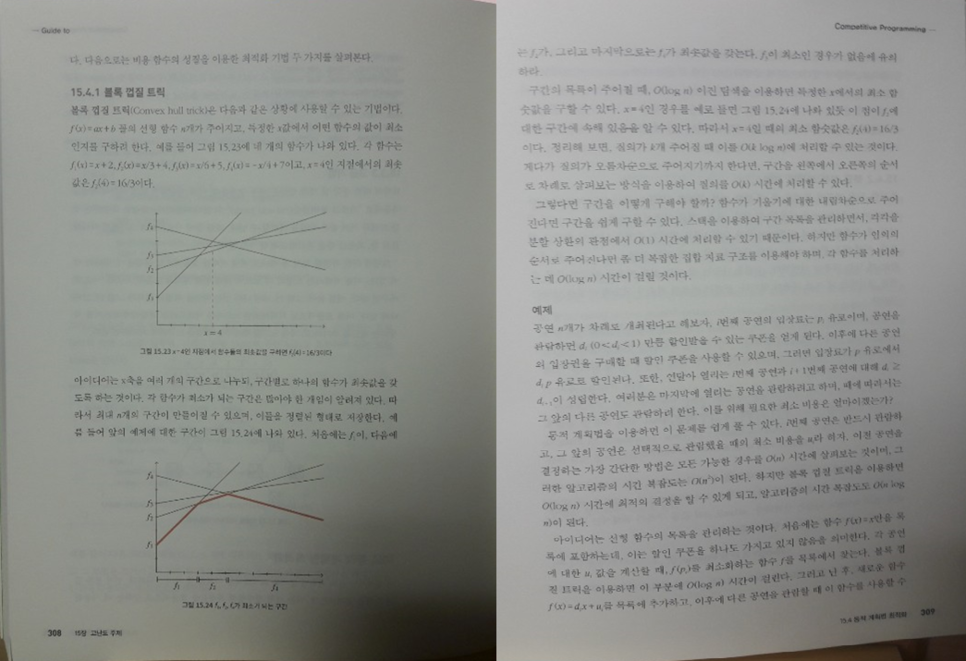
실제 프로그래밍 대회에서 출제되는 유형이지만 평소에는 자주 다루어보지 못한 주제들을 이 책에서는 다루고 있습니다. 위 두 가지 부분은 책을 읽으면서 굉장히 만족했던 부분입니다. 평소에 공부할 때는 내용에 대한 부분과 활용법에 대해서 일일이 인터넷으로 찾아봐야 했는데, 책에서 전반적으로 다루어주고 있어서 가장 좋았던 부분이었습니다.
3. 책 소감
책을 읽고 난 소감을 말하자면 C++을 모르거나 공부의지가 약한 분들은 읽기가 힘들 것 같습니다. 책의 소개에서는 초보자에게도 적합한 책이라고 설명되어 있지만 저는 초보자가 읽기에는 조금 벅차지 않을까 생각합니다.
첫째로, 방대한 양을 다루다 보니깐 책의 깊이나 자세함은 조금 떨어지는 것 같습니다. 3개월 동안 알고리즘 공부하면서 봤던 내용이 이 책에서 반이고 그렇지 않은 내용이 반이었습니다. 그렇기에 알고리즘을 처음 준비하시는 분들이나 공부의지가 약하신 분들은 입문서로 이 책을 시작하기에는 조금 무리가 있을 것 같습니다. 내용이 방대하기 때문에 쉽게 지칠 수 있고, 설명이 이해가 안 가면 쉽게 포기할 수 있기 때문입니다. 하지만 주제가 방대하기 때문에 의지가 있으신 분들은 다른 참고서를 참고하면서 공부하면 프로그래밍 대회에서 나오는 모든 주제를 다룰 수 있을 것 같습니다.
둘째로, C++에 대한 설명이 없고 특정 부분에서는 라이브러리를 사용해서 설명합니다. 그렇기에 파이썬을 2년 가까이 사용한 입장에서도 코드가 친숙하지 않은 부분들이 있었습니다. 그러한 부분은 찾아보면서 읽으면 이해가 가긴 했지만 첫 번째 이유에서 말했다 싶이 시간이 좀 오래 걸렸고 지루했기 때문입니다.
하지만 그렇지 않은 분들이라면 세 가지 이유로 책을 읽는 것을 추천드립니다.
첫째, 위에서도 말했지만 다양한 풀이를 제공합니다. 위의 최대 부분 합 예제를 제외하고도 두 퀸이라는 문제가 주어지면 풀이로, (1) 모든 경우의 수 (2) 그룹 단위로 묶는 방법 (3) 점화식 세우기로 총 3가지 방법을 설명합니다. 대부분의 책이 한 가지의 방법으로 풀이를 제공하는 것에 반해 위의 방법은 프로그래밍 대회를 준비하는 것에 매우 좋은 공부 방법이라 생각합니다.
둘째, 다루는 주제가 다양합니다. 책의 옮긴이의 글에 "최근에 출제된 문제에서 꽤 등장하지만, 아직 블로그 등에서만 접할 수 있는 주제도 포함되어 있어 유용한 참고 자료로 쓰일 수 있을 것입니다"라는 말이 나오는데, 책을 다 읽고 보니 정말 공감되는 말이었습니다. 제가 공부했던 자료에서는 설명되지 않았지만 문제풀이하면서 봤던 내용들이 이 책에는 설명되어 있었습니다.
셋째, 프로그래밍 대회에 필요한 수학, 주제, 활용, 효율성에 대해 중점적으로 설명해주기 때문에 프로그래밍 대회에 참가할 목적으로 매우 좋은 책이라고 생각합니다. 위의 내용에서도 코드의 효율성에 대해 많은 부분에서 다루고 있습니다. 그렇기 때문에 꼭 대회 목적이 아니어도 자신의 코드를 향상시키기에 좋다고 생각합니다.
4. 결론
최근 IT기업에서 코딩 테스트는 필수적이고 삼성이나 구글과 같은 특정 기업은 알고리즘을 잘하는 사람을 우대하는 모습을 보입니다. IT기업을 준비하는 사람이라면 언젠가 한 번은 알고리즘에 대한 공부를 해야 합니다. 이 책은 다양한 주제를 다루기 때문에 코딩 테스트에서 나올 수 있는 모든 내용을 다룰 수 있다고 생각합니다. 주제가 다양하고, 이해가 가지 않는 부분은 스스로 찾아보고 고민해야 하는 부분이 많을 수 있습니다. 하지만 그 모든 과정을 견디고 책을 끝까지 읽는다면 어떠한 코딩 테스트를 겪든 프로그래밍 대회에 나가든 좋은 성적을 거둘 수 있을 거라 확신합니다.
5. 부록
<알고리즘 트레이닝 : 프로그래밍 대회 입문 가이드> 목차
1장. 들어가며
1.1 경진 프로그래밍이란 무엇인가?
1.2 이 책에 대하여
1.3 CSES 문제 셋
1.4 그 밖의 참고자료
2장. 프로그래밍 기법
2.1 언어적 특성
2.2 재귀적 알고리즘
2.3 비트 연산
3장. 효율성
3.1 시간 복잡도
3.2 예제 문제
4장. 정렬과 탐색
4.1 정렬 알고리즘
4.2 정렬을 이용한 문제 풀이
4.3 이진 탐색
5장. 자료 구조
5.1 동적 배열
5.2 집합 자료 구조
5.3 실험
6장. 동적 계획법
6.1 기본 개념
6.2 다른 예제
7장. 그래프 알고리즘
7.1 그래프 기본
7.2 그래프 순회
7.3 최단 경로
7.4 사이클 없는 방향 그래프
7.5 후속 노드 그래프
7.6 최소 신장 트리
8장. 알고리즘 설계 기법
8.1 비트 병렬 알고리즘
8.2 분할 상환 분석
8.3 최솟값 구하기
9장. 구간 질의
9.1 정적 배열에 대한 질의
9.2 트리형 자료 구조
10장. 트리 알고리즘
10.1 기본 기술
10.2 트리 질의
10.3 고급 기술
11장. 수학
11.1 정수론
11.2 조합론
11.3 행렬
11.4 확률
11.5 게임 이론
12장. 고급 그래프 알고리즘
12.1 그래프의 강결합성
12.2 완전 경로
12.3 최대 유량
12.4 깊이 우선 탐색 트리
13장. 기하
13.1 기하 기법
13.2 스윕 라인 알고리즘
14장. 문자열 알고리즘
14.1 기본 주제
14.2 문자열 해싱
14.3 Z알고리즘
14.4 접미사 배열
15장. 고난도 주제
15.1 제곱근 기법
15.2 구간 트리 다시 살펴보기
15.3 트립
15.4 동적 계획법 최적화
15.5 그 밖의 기법
부록A. 수학적 배경이론
'개인 공간 > 리뷰' 카테고리의 다른 글
| [나는 리뷰어다] 스파크를 활용한 실시간 처리 (0) | 2021.05.23 |
|---|---|
| [나는 리뷰어다] Learning SQL (러닝 SQL) (0) | 2021.04.18 |
| [나는 리뷰어다] GAN 첫걸음 (0) | 2021.03.21 |
| [나는 리뷰어다] 진지한 파이썬 (2) | 2021.02.16 |
| 케라스 창시자에게 배우는 딥러닝 (0) | 2019.07.20 |




